Метод пирамидальной сортировки, изобретенный Д. Уилльямсом, является улучшением традиционных сортировок с помощью дерева.
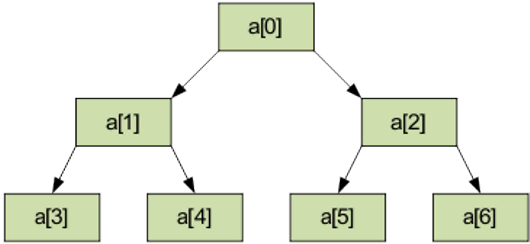
Пирамидой (кучей) называется двоичное дерево такое, что
a[i] ≤ a[2i+1];
a[i] ≤ a[2i+2].
Подробнее
a[0] — минимальный элемент пирамиды.
Общая идея пирамидальной сортировки заключается в том, что сначала строится пирамида из элементов исходного массива, а затем осуществляется сортировка элементов.
Выполнение алгоритма разбивается на два этапа.
1 этап Построение пирамиды. Определяем правую часть дерева, начиная с n/2-1 (нижний уровень дерева). Берем элемент левее этой части массива и просеиваем его сквозь пирамиду по пути, где находятся меньшие его элементы, которые одновременно поднимаются вверх; из двух возможных путей выбираете путь через меньший элемент.
Например, массив для сортировки
24, 31, 15, 20, 52, 6
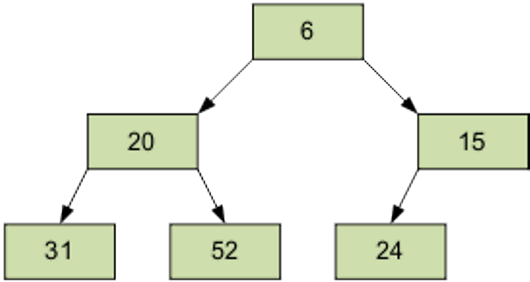
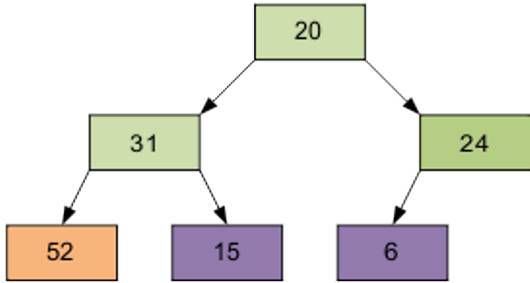
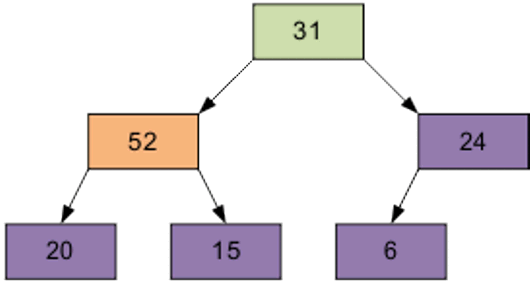
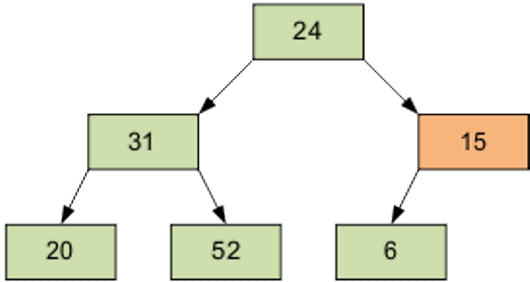
Расположим элементы в виде исходной пирамиды; номер элемента правой части (6/2-1)=2 — это элемент 15.
Результат просеивания элемента 15 через пирамиду.
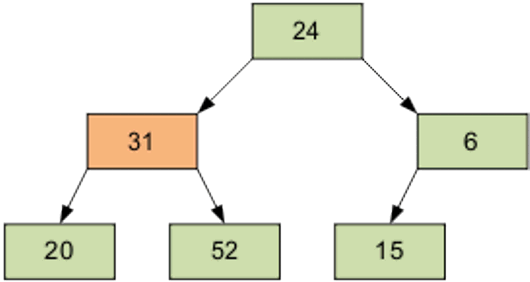
Следующий просеиваемый элемент – 1, равный 31.
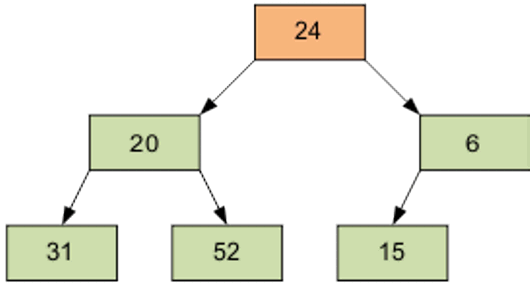
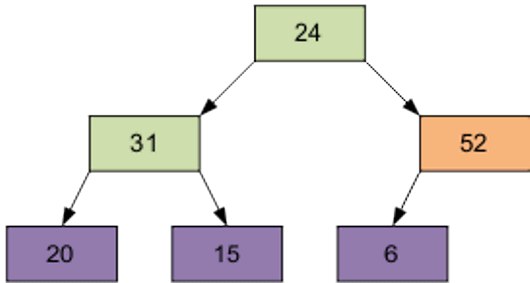
Затем – элемент 0, равный 24.
Разумеется, полученный массив еще не упорядочен. Однако процедура просеивания является основой для пирамидальной сортировки. В итоге просеивания наименьший элемент оказывается на вершине пирамиды.
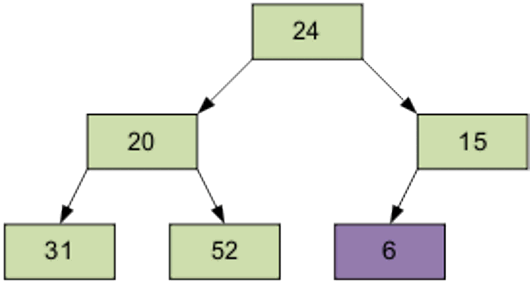
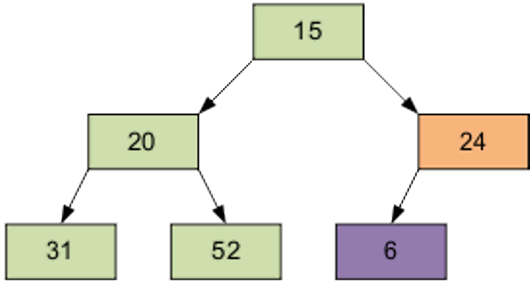
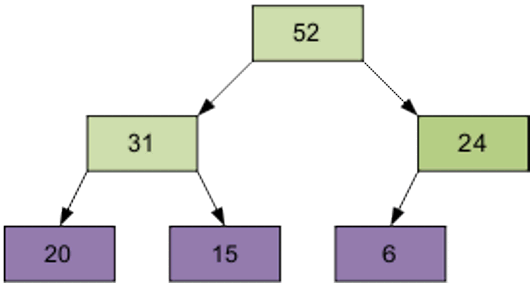
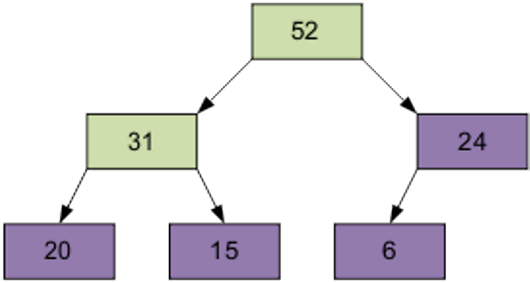
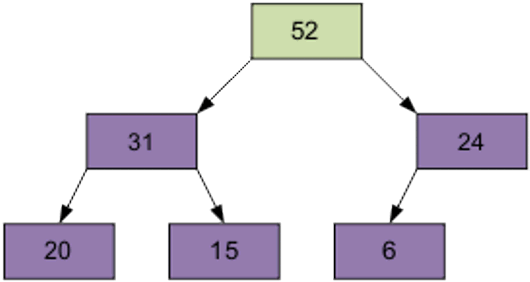
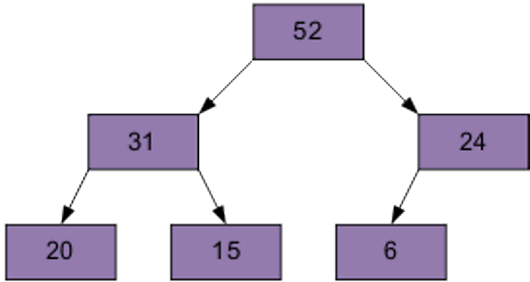
2 этап Сортировка на построенной пирамиде. Берем последний элемент массива в качестве текущего. Меняем верхний (наименьший) элемент массива и текущий местами. Текущий элемент (он теперь верхний) просеиваем сквозь n-1 элементную пирамиду. Затем берем предпоследний элемент и т.д.
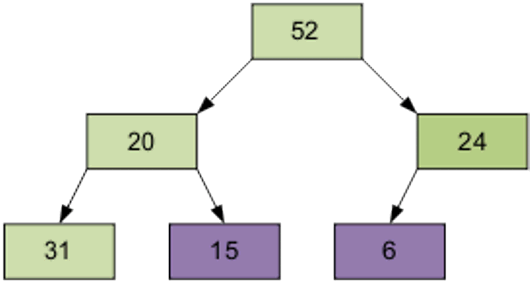
Продолжим процесс. В итоге массив будет отсортирован по убыванию.
Реализация пирамидальной сортировки на Си
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdlib.h>
// Функция "просеивания" через кучу - формирование кучи
void siftDown(int *numbers, int root, int bottom)
{
int maxChild; // индекс максимального потомка
int done = 0; // флаг того, что куча сформирована
// Пока не дошли до последнего ряда
while ((root * 2 <= bottom) && (!done))
{
if (root * 2 == bottom) // если мы в последнем ряду,
maxChild = root * 2; // запоминаем левый потомок
// иначе запоминаем больший потомок из двух
else if (numbers[root * 2] > numbers[root * 2 + 1])
maxChild = root * 2;
else
maxChild = root * 2 + 1;
// если элемент вершины меньше максимального потомка
if (numbers[root] < numbers[maxChild])
{
int temp = numbers[root]; // меняем их местами
numbers[root] = numbers[maxChild];
numbers[maxChild] = temp;
root = maxChild;
}
else // иначе
done = 1; // пирамида сформирована
}
}
// Функция сортировки на куче
void heapSort(int *numbers, int array_size)
{
// Формируем нижний ряд пирамиды
for (int i = (array_size / 2); i >= 0; i--)
siftDown(numbers, i, array_size - 1);
// Просеиваем через пирамиду остальные элементы
for (int i = array_size - 1; i >= 1; i--)
{
int temp = numbers[0];
numbers[0] = numbers[i];
numbers[i] = temp;
siftDown(numbers, 0, i - 1);
}
}
int main()
{
int a[10];
// Заполнение массива случайными числами
for (int i = 0; i<10; i++)
a[i] = rand() % 20 - 10;
// Вывод элементов массива до сортировки
for (int i = 0; i<10; i++)
printf("%d ", a[i]);
printf("\n");
heapSort(a, 10); // вызов функции сортировки
// Вывод элементов массива после сортировки
for (int i = 0; i<10; i++)
printf("%d ", a[i]);
printf("\n");
getchar();
return 0;
}
Результат выполнения
Анализ алгоритма пирамидальной сортировки
Несмотря на некоторую внешнюю сложность, пирамидальная сортировка является одной из самых эффективных. Алгоритм сортировки эффективен для больших n. В худшем случае требуется n·log2n шагов, сдвигающих элементы. Среднее число перемещений примерно равно
(n/2)·log2n,
и отклонения от этого значения относительно невелики.
Назад: Алгоритмы сортировки и поиска
Комментариев к записи: 30