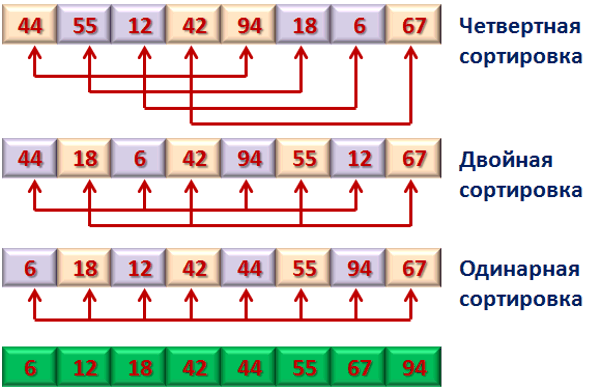
В 1959 г. Д. Шеллом было предложено усовершенствование сортировки с помощью прямого включения.
Сначала отдельно группируются и сортируются элементы, отстоящие друг от друга на 4 позиции. Такой процесс называется четвертной сортировкой.
После первого прохода элементы перегруппировываются — теперь каждый элемент группы отстоит от другого на 2 позиции — и вновь сортируются (двойная сортировка).
На третьем проходе идет обычная сортировка.
Кажется, что необходимость нескольких проходов сортировки, в каждом из которых участвуют все элементы, потребует большего количества машинных ресурсов, чем обычная сортировка. Однако на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены и требуется сравнительно немного перестановок.
Такой метод в результате дает упорядоченный массив, и каждый проход от предыдущих только выигрывает (так как каждая i-сортировка объединяет две группы, уже отсортированные 2i-сортировкой).
Расстояния в группах можно уменьшать по-разному, лишь бы последнее было единичным. В самом плохом случае последний проход сделает всю работу.
Реализация сортировки Шелла на Си
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#define _CRT_SECURE_NO_WARNINGS // для корректной работы scanf()
#include <stdio.h>
#define SIZE 10
// Функция сортировки Шелла
void shellSort(int* num, int size)
{
int increment = 4; // начальное приращение сортировки
while (increment > 0) // пока существует приращение
{
for (int i = 0; i < size; i++) // для всех элементов массива
{
int j = i; // сохраняем индекс и элемент
int temp = num[i];
// просматриваем остальные элементы массива, отстоящие от j-ого
// на величину приращения
while ((j >= increment) && (num[j - increment] > temp))
{ // пока отстоящий элемент больше текущего
num[j] = num[j - increment]; // перемещаем его на текущую позицию
j = j - increment; // переходим к следующему отстоящему элементу
}
num[j] = temp; // на выявленное место помещаем сохранённый элемент
}
if (increment > 1) // делим приращение на 2
increment = increment / 2;
else if (increment == 1) // последний проход завершён,
break; // выходим из цикла
}
}
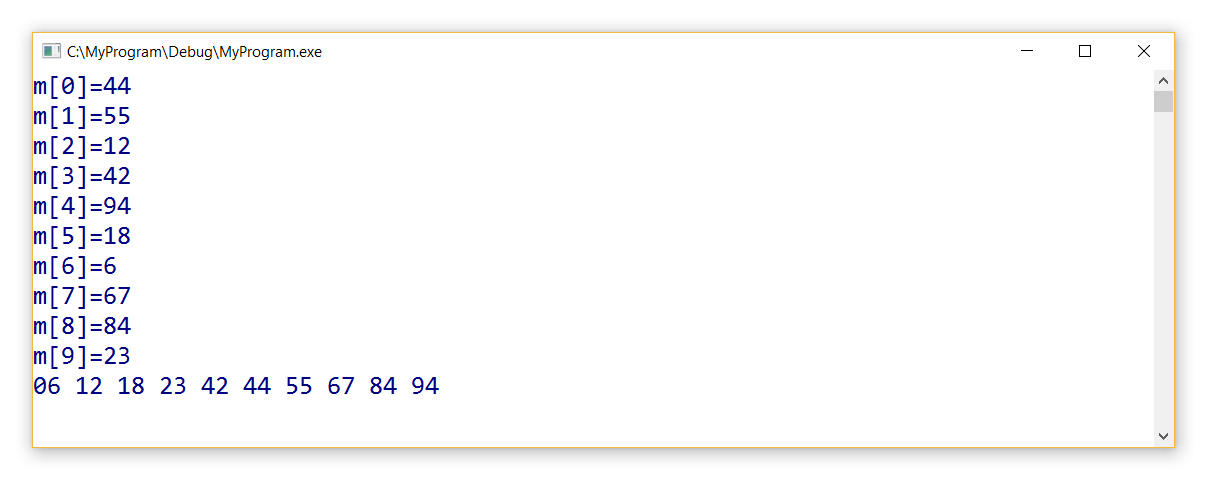
int main()
{
int m[SIZE];
// Вводим элементы массива
for (int i = 0; i< SIZE; i++)
{
printf("m[%d]=", i);
scanf("%d", &m[i]);
}
shellSort(m, SIZE); // вызываем функцию сортировки
// Выводим отсортированные элементы массива
for (int i = 0; i< SIZE; i++)
printf("%.2d ", m[i]);
getchar(); getchar();
return 0;
}
Анализ алгоритма
Приводимая программа не ориентирована на некую определенную последовательность расстояний. Все t расстояний обозначаются соответственно
{\displaystyle{h_1, h_2, …, h_t}}
для них выполняются условия
{\displaystyle \left\{{\begin{array}{lcr}h_t=1\\ h_{i+1} \lt h_i \\\end{array}}\right.}
Каждая {h}-сортировка программируется как сортировка с помощью прямого включения.
В алгоритме неизвестно, какие расстояния дают наилучшие результаты.
Дональд Кнут рекомендует такую последовательность:
1, 3, 7, 15, 31, …,
то есть
{\displaystyle \left\{ {\begin{array}{lcr}h_{k-1}=2 \cdot h_k + 1\\ h_t = 1 \\ t = log_2 n — 1 \\\end{array}} \right. }